📘 插入排序
介绍
插入排序是一种对于少量元素排序非常有效的排序算法,在日常生活中最常见的例子就是插入扑克牌,我们总是喜欢将某张扑克牌插入到已排序的扑克中。
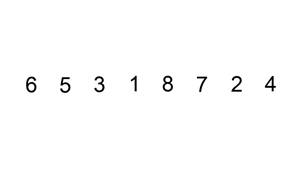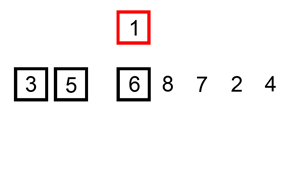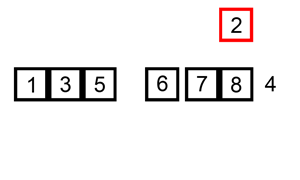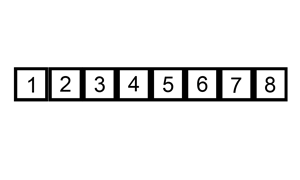
实现
关于插入排序的使用可查看API/排序/insertionSort,插入排序的JavaScript实现如下:
import comparator from '../../utils/comparator/_comparator'
/**
* @since: 2019-08-14 10:18:17
* @description: 插入排序
* @param: {Array} originalArray 需要排序的数组
* @param: {Function(a: *, b: *)} customComparator 自定义比较方法
* @returns: {Array} 返回一个新的排序后的数组
*/
function insertionSort (originalArray, customComparator) {
const array = [...originalArray]
let currentElement, preIndex
// 设置自定义比较方法
comparator.setCompare(customComparator)
for (let i = 1; i < array.length; i++) {
preIndex = i - 1
// 当前需要排序的元素(第一个元素默认已经排好序)
currentElement = array[i]
// 判断前一个元素是否大于当前元素,如果是则前一个元素往后移
// 直到不存在前一个元素或者前一个元素小于当前元素,则停止移动
while (preIndex >= 0 && comparator.greaterThan(array[preIndex], currentElement)) {
array[preIndex + 1] = array[preIndex--]
}
// 将当前排序元素插入到移动后的位置
array[preIndex + 1] = currentElement
}
return array
}
证明
说明
循环不变式:在for循环的每次迭代开始时,元素array[0] ~ array[j-1]始终是原数组的元素,且是一个排序好的子数组。以[6,5,3,1,8,7,2,4]为例,第一次循环默认[6]就是已经排序好的子数组,那么第二次循环[5,6]就是已经排序好的子数组,我们称这样的子数组为循环不变式。
循环不变式可以帮助理解算法的正确性。关于循环不变式必须证明三条性质:
- 初始化:循环的第一次迭代之前,它为真。
- 保持:循环的某次迭代之前它为真,那么下次迭代之前它仍然为真。
- 终止:在循环终止时,不变式有助于证明算法的正确性。
以[6,5,3,1,8,7,2,4]应用于插入排序证明该排序的正确性:
- 初始化:当
i = 1时,循环不变式为array[0] ~ array[1-0],即第一次迭代之前的循环不变式为原数组的[6],在子数组只有一个元素的前提下,该元素默认可以归为已经排序好的元素,表明第一次迭代之前循环不变式成立。 - 保持:非形式化的插入第
i个元素,将array[i-1]、array[i-2]、array[i-3]等向右移动一个位置,直到找到array[i]的合适位置进行插入操作。首先,移动后的arrary[0] ~ array[i]仍然是移动前的元素array[0] ~ array[i],只是元素的位置发生了变化。其次,此前array[0] ~ array[i-1]是一个排序好的数组,那么array[0] ~ array[i]仍然是一个排序好的数组。因此,下一次循环迭代增加i循环不变式仍然保持不变。 - 终止:在循环终止时,由
i <= array.length - 1可以确定终止条件为i = array.length,此时说明数组array[0] ~ array [array.length-1]是原来数组的所有元素,且已经按序排列,因此算法正确。
小结
介绍插入排序算法,证明该算法能正确的排序。
📙 插入排序习题 →